突然间，十月以某种始料未及的方式结束了，也许是因为今年雨水变多的缘故，总觉得这个秋天过去得平平无奇，仿佛只有观音禅寺的满地银杏叶儿，真正地宣布着秋天的到来，直到看见朋友在朋友圈里借景抒怀，『 霜叶红于二月花 』，秋天终于没能迁就我的一厢情愿，我确信她真的来了。当然，秋天不单单会带来这些诗情画意的东西，更多的时候我们听到的是双十一、双十二，这些曾经由光棍节而催生出的营销活动，在过去的十多年间渐渐成为了一种文化现象，虽然我们的法定节日永远都只有那么几天，可这并不妨碍我们自己创造出无数的节日，从那一刻开始，每个节日都可以和购物产生联系，这种社会氛围让我们有了某种仪式感，比如，零点时为了抢购商品恨不得戳破屏幕。再比如，在复杂的满减、红包、优惠券算法中复习数学知识。可当时间节点来到 1202 年，你是否依然对剁手这件事情乐此不疲呢，在新一轮剁手行动开始前，让我们来试试通过 Python 预测一下今年的交易额，因为在这场狂欢过后，没有人会关心你买了什么，而那个朴实无华的数字，看起来总比真实的人类要生动得多。

思路说明

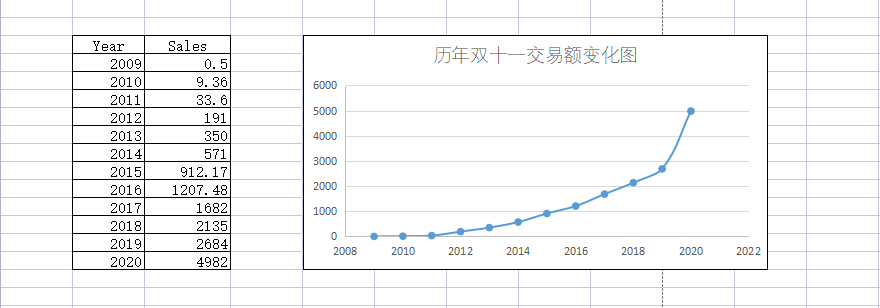
其实，我一直觉得这个东西，完全不需要特意写一篇文章，因为用毕导的话说，这个东西我们在小学二年级就学过。相信只要我说出 最小二乘法 和 线性回归 这样两个关键词，各位就知道我在说什么了！博主从网上收集了从 2009 年至今历年双十一的交易额数据，如果我们将其绘制在二维坐标系内，就会得到一张散点图，而我们要做的事情，就是找到一条曲线或者方程，来对这些散点进行拟合，一旦我们确定了这样一条曲线或者方程，我们就可以预测某一年双十一的交易额。如图所示，是 2009 年至今历年双十一的交易额数据，在 Excel 中我们可以非常容易地得到对应的散点图：

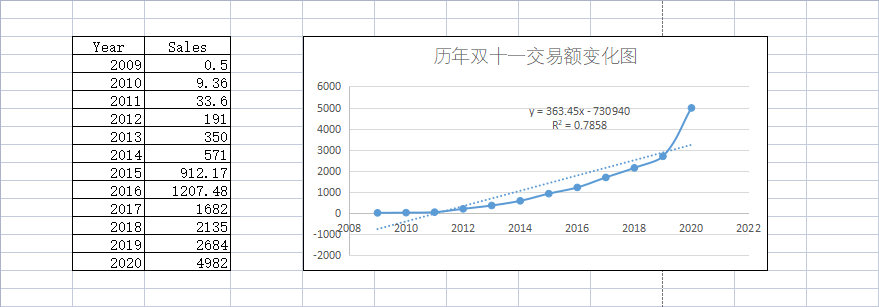
如果有朋友做过化学或者生物实验，对接下来的事情应该不会感到陌生，通常我们会在这类图表中添加趋势线，由此得到一个公式，实际上这就是一个回归或者说拟合的过程，因为 Excel 内置了线性、指数型、对数型等多种曲线模型，所以，我们可以非常容易地切换到不同的曲线，而评估一个方程好坏与否的指标为 $R^2$，该值越接近 1 表示拟合效果越好，如图是博主在 Excel 中得到的一条拟合方程：

那么，在 Python 中我们如何实现类似的效果呢？答案是 scikit-learn，这是 Python 中一个常用的机器学习算法库，主要覆盖了以下功能：分类、回归、聚类、数据降维、模型选择 和 数据预处理，我们这里主要利用了回归这部分的 LinearRegression 类，顾名思义，它就是我们通常说的线性回归。事实上，这个线性并不是单指一元一次方程，因为我们还可以使用二次或者三次多项式，因为上面的 Excel 图表早已告诉我们，一元一次方程误差太大。

实现过程

OK，具体是如何实现的呢？首先，我们从 CSV 文件中加载数据，这个非常简单，利用 Pandas 库中的 read_csv() 方法即可：

df = pd.read_csv('./历年双十一交易额.csv', index_col = 0)

接下来，我们使用下面的方法来获取 年份 和 交易额 这两列数据：

year = np.array(df.index.tolist())
sales = np.array(df.Sales.tolist())

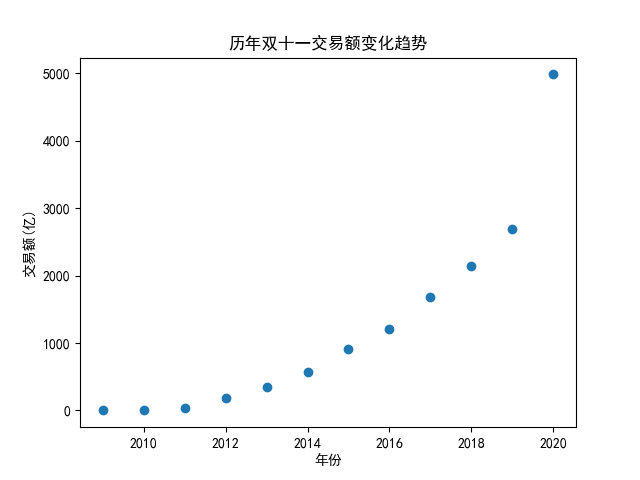
此时，我们可以非常容易地用 matplotlib 库绘制出对应的图表：

plt.scatter(year, sales, marker='o')
plt.xlabel('年份')
plt.ylabel('交易额(亿)')
plt.title('历年双十一交易额变化趋势')

接下来，我们来看看如何对这组数据做线性回归，以一元一次方程为例：

X = (year - 2008).reshape(-1, 1)
X = np.concatenate([X], axis= -1)
Y = sales
lr = LinearRegression()
lr.fit(X, Y)
print('方程系数：', lr.coef_)
print('方程截距：',lr.intercept_)

这里，首先我们需要把 2009 到 2020 这个范围内的年份转化为更方便计算的 1、2、3 …，所以，每一个数都减去了 2008，这样我们就得到了横坐标 X 以及 纵坐标 Y。接下来，我们只需要将其传入 fit() 方法即可。有时候，你可能会看到下面这样的代码，即用于划分 训练集 和 测试集 的的代码片段：

X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3, random_state=0)

考虑到我们这里的样本数据本来就不多，毕竟，这股消费主义的风潮在中国刚刚流行了十二年，所以，我们要珍惜这份福报，就不划分 训练集 和 测试集 了(逃。此时，我们会得到两个重要的参数，即方程系数 lr.coef_ 和 方程截取 lr.intercept_，而一旦有了这两个参数，我们就能确定一个线性方程，即传说中的 $y=ax+b$ :

f = lambda x: lr.coef_[0] * x + lr.intercept_
print('2021年交易额预测：', f(13))

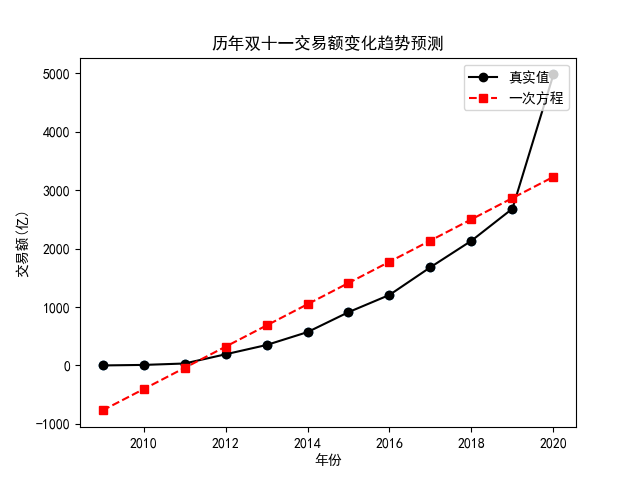
此时，f(13) 就是 2021 年双十一的交易额，显然，这是一个预测值，大概是 3592 亿，这属实是有点离谱啦，都没能超过 2020 年的 4982 亿，我们前面提到过 $R^2$，在 scikit-learn 中我们使用下面的方法来计算它：

print('R^2：', lr.score(X_test, Y_test))

没错，score() 函数需要这样一组测试数据，我们利用前面划分 训练集 和 测试集 的方法就可以得到它。我们发现，这个值大概是 0.73，这要不离谱都说不过去，这一点我们从图上就可以看出来：

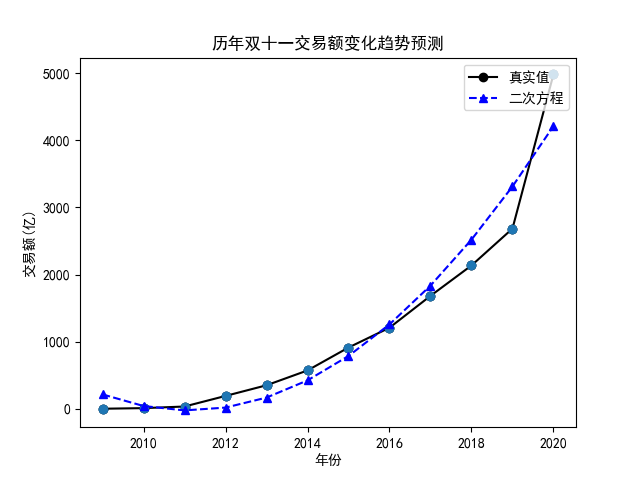
这样显然不行啊，那怎么办呢？遥想古人利用“割圆术”无限逼近圆形进而计算出圆周率的这种执着，我们是不是可以通过提高“次数”来解决欠拟合的问题呢？换句话说，我们来试试一元二次方程，此时，我们只需要调整下横坐标 X 的构造过程：

X = (year - 2008).reshape(-1, 1)
X = np.concatenate([X**2, X], axis= -1)

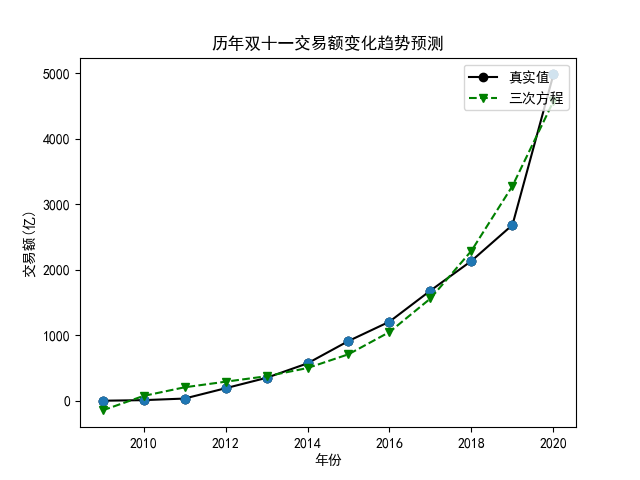
简单来说，如果你需要构造一个 N 次多项式，那么，只需要由高到底依次写出来即可，所以，你可以想象得到，对于三次多项式，我们可以这样构造：

X = (year - 2008).reshape(-1, 1)
X = np.concatenate([X**3, X**2, X], axis= -1)

对于二次多项式，我们可以得到下面的结果，其 $R^2$ 为 0.92，预测 2021 年双十一交易额为 5218 亿：

同理，对于三次多项式，我们可以得到下面的结果，其 $R^2$ 为 0.96，预测 2021 年双十一交易额为 6213 亿：

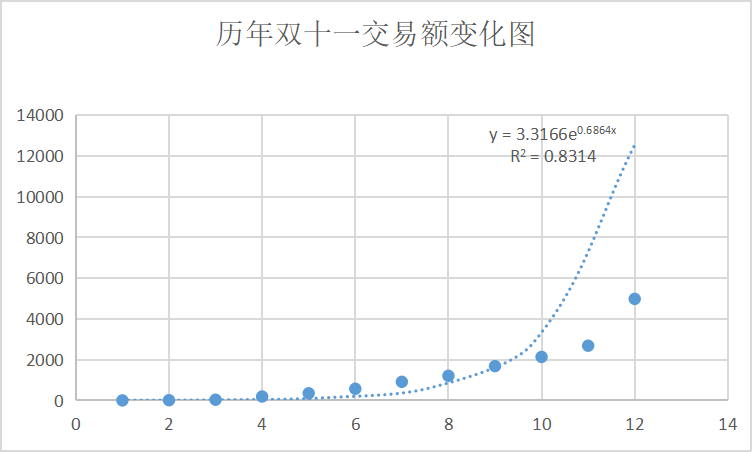
整体上看，三次方程的拟合效果更好一点，达到了 0.96，但这个和大学时候做实验追求的 0.99 相比，多少有一点尴尬，屏幕前的你，是否想到了更好的曲线模型呢，我们常常说某某行业取得了指数级的增长，难道说指数模型更适合这个问题？关于这一点博主没能去亲自验证，因为看起来在 scikit-learn 中没有指数型函数的计算模型，可当博主在 Excel 中添加了指数型的趋势线以后，发现结果有点出人意料，因为它的 $R^2$ 只有 0.8314，而按这个方程计算出的交易额则约为2万多亿，好家伙，这都赶上恒大目前拖欠的债务了，想想就觉得离谱，指数型函数对应的曲线如下：

此时此刻，坐在屏幕前的你，更倾向于选择那种计算模型呢，个人觉得三次方程更好一点，因为它的 $R^2$ 是目前最好的，当然，scikit-learn 还有类似可解释的方差分数、最大误差、平均绝对误差、均方误差、均方误差对数等等不同的指标，大家可以参考 官方文档 来做更进一步的探索，一切都只有等到下个月双十一过后方能揭晓，就让我们拭目以待！本文中使用的源代码，已更新至 Github 供大家参考，如果大家对博客中的内容有什么意见或者建议，欢迎大家在评论区积极留言，谢谢大家！

本文小结

恍惚中惊觉，十月份就这样结束了，这意味是 2021 年只剩下 60 多天。上了年纪的人总不免开始怀念，那些偷偷从树叶间隙里溜走的时光，去年的这个时候我在做些什么呢？大概刚刚追完「半泽直树」第二部吧！在疫情愈发常态化的日子里，人对于未来总有种难以言说的失控感，某君有言道，『不知道明天和意外哪一个先来』，虽然机器学习可以通过“训练”过去达到“预测”未来的目的，可人生并没有哪一个方程可以完美拟合，虽然这个世界早已为你规划好一条叫做“随大流”的路，一个人的过去、当下就像无数个离散的点，这些点构成了我们人生的轨迹，某种我们通常称之为回忆的东西，可这些点是否会向着预期的方向延伸，也许，永远没有人会知道答案，这个世界上有相当多的数字，譬如自然对数、圆周率、黄金分割比等等，都是前辈先哲从自然世界中寻找到的，可对于我们的人生而言，并没有这样明显的答案，所以，每次做数据分析的时候，我都有种奇怪的感觉，因为我不明白这些数字背后，到底和我们本身有着什么样的关联，可这个世界偶尔会感应到你的失落，当你听着「明年今日」，而心里想的是去年今日，我想，这一页可以翻过去，这篇文章可以结尾，这样就可以了吧…