在某个瞬间，我忽然发觉，三体或是AI，本质上是非常相近的事物，甚至在面对任何未知领域的时候，人类总会不自觉地划分为降临派、拯救派和幸存派。姑且不论马斯克等人叫停 GPT-5 的真实动机如何，当大语言模型(LLM)裹挟着 AIGC 的浪潮气势汹汹地袭来时，你是否会像很多人一样，担心有一天会被机器取代以致于失业呢？此前，我曾自嘲般地提到过，我是一名 YAML 工程师、Markdown 工程师、Dockerfile 工程师……，甚至以后还会变成一名 Prompt 工程师，而这背后的因果关系，本质上我们对这个世界的编程方式，正在逐步地从 DSL 转向自然语言。我个人认为，任何低端、重复的工作最终都会被机器取代，而诸如情感、艺术、心理、创意……等非理性领域，则可能会成为人类最后的防线。两年前，柯洁以 0:3 的比分输给 AlphaGo，一度在棋盘前情绪失控，我想，那一刻他大概不会想到两年后还会出现 ChatGPT。在《蜘蛛侠：英雄无归》电影里面，彼得·帕克对奇异博士说，“你知道比魔法更神奇的东西是什么吗？是数学”。我个人非常喜欢这句话，因为在绝对的理性面前，一切的技巧都是徒然，更重要的是，如此深刻的哲理，居然是来自生活中一个真实案例。

电子签章与数学

好的，虽然我们说那些低端、重复的工作最终都会被机器取代，但是真正残酷的现实是，我们并没有那么多需要创造力的工作，就像我们并不需要那么多架构师一样。毕竟，你想象不到，一个人在五年前和五年后做的工作毫无差别，特别是企业级应用中非常普遍的打印。过去这些年，企业数字化转型的口号一直在喊，可到头来我们并没有等来真正的无纸化，企业依然对打印单据这件事情乐此不疲，仿佛没有这一张纸业务就没法开展一样。在这个过程中，企业会希望你能在单据上加盖公司的印章，这就产生了所谓的“电子签章”的需求。当然，我们这里不考虑电子签章的申请、加/解密、防伪等实际的流程，我们只是考虑将其通过 GDI+ 绘制出来即可。考虑到印章有圆形和椭圆形两种形制，所以，我们下面来进行分类讨论。

圆形印章

可以注意到，圆形印章通常由四部分组成，分别是顶部文字、中心部分的五角星、中下部分文字和底部文字。

其中，顶部文字表示印章所属的公司/组织/机构，底部文字表示14位印章编号，这两部分文字均呈圆弧状分布。具体该如何实现呢？我们来一起看一下。首先，圆形印章的轮廓是一个标准的圆形，这个绘制非常容易：

// 从位图创建一个画布
var bitmap = new Bitmap(width, height, PixelFormat.Format32bppArgb);
var g = Graphics.FromImage(bitmap);

// 绘制圆形边框 
var rect = new RectangleF(x, y, radius, radius);
var Pen pen = new Pen(Color.Red, 3.0f);
g.DrawEllipse(pen, rect);

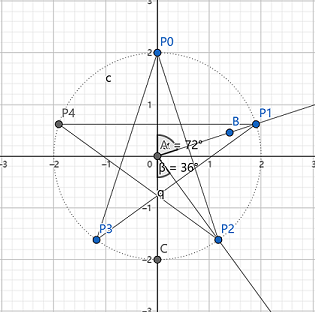
而对于中心部分的五角星，我们使用一个路径填充即可。此时，问题的关键是在圆上找出五角星的五个顶点。显然，五角星的顶点满足下面的几何关系：

利用三角函数的知识，我们可以非常容易地写出对应代码，请注意，计算机中使用的坐标系 Y 轴正方向向下：

var Radius = rect.Width / 2 * 0.45;
var Center = new PointF(rect.X + rect.Width / 2, rect.Y + rect.Height / 2);
PointF[] points = new PointF[]
{
    // P0
    new PointF(Center.X, (float)(Center.Y - Radius)),
    // P1
    new PointF(
        (float)(Center.X + Radius * Math.Sin(72 * Math.PI / 180)), 
        (float)(Center.Y - Radius * Math.Cos(72 * Math.PI / 180))
    ),
    // P2
    new PointF(
        (float)(Center.X + Radius * Math.Sin(36 * Math.PI / 180)), 
        (float)(Center.Y + Radius * Math.Cos(36* Math.PI / 180))
    ),
    // P3
    new PointF(
        (float)(Center.X - Radius * Math.Sin(36 * Math.PI / 180)),
        (float)( Center.Y + Radius * Math.Cos(36 * Math.PI / 180))
    ),
    // P4
    new PointF(
        (float)(Center.X - Radius * Math.Sin(72 * Math.PI / 180)), 
        (float)(Center.Y - Radius * Math.Cos(72 * Math.PI / 180))
    ),
};

// 根据五个点生成一个封闭路径
var path = new GraphicsPath(FillMode.Winding);
path.AddLine(points[0], points[2]);
path.AddLine(points[2], points[4]);
path.AddLine(points[4], points[1]);
path.AddLine(points[1], points[3]);
path.AddLine(points[3], points[0]);
path.CloseFigure();

// 填充路径
g.RotateTransform(0);
g.FillPath(new SolidBrush(Color.Red), path);

接下来，我们来考虑如何绘制这两段呈圆弧状分布的文字，这里需要用到的数学知识是圆的参数方程以及三角函数。其基本思路是：选定一个起始角度，再根据总角度和文字数目计算一个步长，进而确定每一个文字对应的角度。譬如，这里假定上半部分圆弧总角度为300 度，下半部分圆弧总角度为 60 度：

var center = new PointF(rect.X + rect.Width / 2.0f, rect.Y + rect.Height / 2.0f);
var fontToFit = new Font("宋体", 13, FontStyle.Bold, GraphicsUnit.Pixel);
var totalAngle = Math.PI * 5 / 3;
var stepAngle = totalAngle / (text1.Length + 1);
var startAngle = Math.PI * 4 / 3;
for (int i = 0; i < text.Length; i++)
{
    float angle = (float)(startAngle - (i + 1) * stepAngle);
    if (angle < 0) angle += (float)Math.PI * 2;
    var point = new PointF(
        center.X + radius * (float)Math.Cos(angle), 
        center.Y - radius * (float)Math.Sin(angle)
    );

    g.DrawString(text1[i].ToString(), fontToFit1, brush, point.x, point.y);
}

我们知道，在三角函数定义中，逆时针方向为正方向，所以，对于上半部分的弧形文字，只需要用起始角度依次减去对应的步长数。为了让后续计算角度的时候更方便一点，这里会将负角统一转换为正角。接下来的事情就顺理成章啦，因为你可以利用三角函数计算出对应的坐标，此时，我们只需要在指定的位置调用 DrawString 函数将每个字符绘制出来即可：

不过，你很快会发现一个问题，那就是这些文字的方向并没有像一般印章那样，始终“正对”着你的实现。此时，你会用到第三个数学知识，即：当一个点变为原点以后，它与 X 轴正方向的夹角会如何变化？你为什么需要这个知识呢？因为我们需要对每个字符做一次平移变换、一次旋转变换，这样才能达到我们的目的，即：无论你从哪一个方向去看这些文字，它对你来说都是“正”的，其代码实现如下：

var center = new PointF(rect.X + rect.Width / 2.0f, rect.Y + rect.Height / 2.0f);
var fontToFit = new Font("宋体", 13, FontStyle.Bold, GraphicsUnit.Pixel);
var totalAngle = Math.PI * 5 / 3;
var stepAngle = totalAngle / (text1.Length + 1);
var startAngle = Math.PI * 4 / 3;
for (int i = 0; i < text.Length; i++)
{
    float angle = (float)(startAngle - (i + 1) * stepAngle);
    if (angle < 0) angle += (float)Math.PI * 2;
    var point = new PointF(
        center.X + radius * (float)Math.Cos(angle), 
        center.Y - radius * (float)Math.Sin(angle)
    );

    g.TranslateTransform(point.X, point.Y);
    var transformAngle = (float)(angle * 180 / Math.PI + 90);
    if (transformAngle > 360) transformAngle -= 360;

    // 注意：RotateTransform() 方法旋转方向是顺时针方向，所以，要用 360 度减去当前角度
    // 印章上方的文字需要正对着外侧，所以，要再加上 180 度
    transformAngle = 360 - transformAngle + 180;
    g.RotateTransform(transformAngle);
    g.DrawString(text[i].ToString(), fontToFit, brush, 0, 0, format);
    g.ResetTransform();
}

这里的关键是 TranslateTransform() 和 RotateTransform() 两个方法，这就是我们上文中提到的平移变换和旋转变换。为什么要这样处理呢？因为我们希望的看到是，文字旋转到“正确”的方向且保持位置不变，如果没有平移转换的话，它会就变成点 A 围绕点 B 旋转，这样显示不符合我们的预期。总之，当一切都在向着预期的方向发展的时候，我们就可以利用这个技巧“照葫芦画瓢”，需要注意的是，底部弧形文字的“正方向”是向下的，因此，在做旋转变换的时候，两者会相差 180 度。对此，我想说，数学真的好用：

相比之下，绘制中下部分文字就非常简单啦，因为它是在一个矩形范围上绘制，你唯一需要的就只有一个勾股定理。理论上，你只要将以上代码片段整合起来，就可以绘制出一个相对完美的印章，我个人踩坑的体会是：真正的困难常常是印章的实际尺寸、打印尺寸、DPI、分辨率这些客观因素。

椭圆形印章

好了，接下来再说椭圆形印章的绘制，原理基本相同，对应的数学知识是椭圆的参数方程。不知道大家是否还记得圆锥曲线、离心率、焦点等概念，博主在写这篇博客的时候，的确是回过头再次重温了这些知识。作为一名程序员，平时没少被别人“教育”业务的重要性，可对我来说，业务大概就是朝三暮四、朝秦暮楚的代名词，相比这些人为想象和构筑的东西，我更喜欢风、沙、星辰这些接近自然和宇宙的东西，对我来说，数学便是如此。好了，下面是绘制弧形文字的代码片段，供大家参考：

var a = rect.Width / 2 * 0.8f;
var b = rect.Height / 2 * 0.8f;
var center = new PointF(rect.X + rect.Width / 2.0f, rect.Y + rect.Height / 2.0f);
var fontToFit = new Font("宋体", 13, FontStyle.Bold, GraphicsUnit.Pixel);
var totalAngle = Math.PI * 5 / 3
var stepAngle = totalAngle / (text1.Length + 1);
var startAngle = Math.PI * 4 / 3
for (int i = 0; i < text.Length; i++)
{
    float angle = (float)(startAngle - (i + 1) * stepAngle);
    if (angle < 0) angle += (float)Math.PI * 2;

    // 利用椭圆参数方程计算坐标
    var point = new PointF(
        center.X + a * (float)Math.Cos(angle), 
        center.Y - b * (float)Math.Sin(angle)
    );

    g.TranslateTransform(point.X, point.Y);
    var transformAngle = (float)(angle * 180 / Math.PI + 90);
    if (transformAngle > 360) transformAngle -= 360;

    // 注意：RotateTransform() 方法旋转方向是顺时针方向，所以，要用 360 度减去当前角度
    // 印章上方的文字需要正对着外侧，所以，要再加上 180 度
    transformAngle = 360 - transformAngle + 180;
    g.RotateTransform(transformAngle);
    g.DrawString(text[i].ToString(), fontToFit1, brush, 0, 0, format);
    g.ResetTransform();
}

可以看出，本质上只需要用半长轴 a 和半短轴 b 替换半径即可。考虑到圆是椭圆的特殊形式，这种从特殊到一般的认知方式，难道不显得有趣吗？同样地，这里提供一个椭圆形印章的效果图：

至此，关于如何通过 GDI+ 绘制印章，笔者可谓是倾囊相授啦，在这个过程中，我最享受的环节，恰恰是那些再寻常不过的数学知识，当你觉得 AI 有一天一定会取代人类的时候，我以为，这代表着绝对理性的胜利，就像令柯洁落泪的 AlphaGo 一样，没有任何技巧，它只是在经历无数次计算以后得出的必然结果，从某种意义上来讲，数学反而是宇宙间最简单的学问，不是吗？如果说人工智能里还有哪些更接近“玄学”的东西，我以为，大概是我们自始至终都没能解释清楚，模仿神经元的神经网络到底是怎样一步步地产生了“意识”？而这一切就好比，你的确知道 ChatGPT 给了你一个满意的答案，但你始终不知道的是，它到底是在经过了一个什么样的思考过程以后，才能给出一个如此契合你心理预期的答案？恍惚之间，我会觉得它符合人类眼中的“高情商”标准，即使它对你一无所知，可它还是能讲出令你“舒服”的话语，如果语言本身就充满了这种迷惑性，那么人类最看重的情感到底又算什么？

字体自适应方案

好了，现在让我们来考虑得更长远一点，当我们实现了一个相对通用的印章绘制算法以后，我们会希望通过配置这些文字来生成不同的印章。此时，一个新的问题产生了：在印章尺寸固定(有相关标准)的情况下，如何能兼容不同长度的文字？一个容易想到的方案是修改字体大小。譬如，当文字较多的时候就缩小字体，当文字较少时就放大字体。所以，下面我想分享的是动态调整字体大小实现字体自适应。

基于宽高

第一种方案基于宽高，即字体是绘制在一个矩形区域内，印章的中下部分通常用来表示印章的用途，此时，我们可以利用 MeasureString 这个方法来测量整个字符串的宽度，并将其和当前矩形的宽度进行比较。如果实际宽度大于当前矩形的宽度，则需要减小字号；如果实际宽度小于当前矩形的宽度，则需要增加字号。当然，缩小的时候可以给一个最小字号，因为你要确保别人能看清印章上的文字；放大的时候需要考虑矩形的高度，因为你要确保印章上的元素不会相互重叠。下面是一个基本实现：

float ScaleFontSizeByContainerSize(Graphics g, string text, Font font, SizeF size) {
    var fontSize = font.Size;

    // 对字体缩小时需要考虑最小的字体大小
    var measuredSize = g.MeasureString(text, new Font(font.FontFamily, fontSize));
    while (measuredSize.Width > size.Width) {
        fontSize -= 0.5f;
        if (fontSize <= MIN_FONT_SIZE) break;
        measuredSize = g.MeasureString(text, new Font(font.FontFamily, fontSize));
    }

    // 对字体放大时需要考虑高度的问题
    measuredSize = g.MeasureString(text, new Font(font.FontFamily, fontSize));
    while (measuredSize.Width < size.Width && measuredSize.Height < size.Height) {
        fontSize += 0.5f;
        measuredSize = g.MeasureString(text, new Font(font.FontFamily, fontSize));
    }

    return fontSize;
}

如图所示，下图展示了相同尺寸下，文字根据字数的多少按不同的字号动态进行缩放：

基于周长

第二种方案基于周长，主要是针对印章中呈圆弧状分布的这些文字，此时，宽度和高度不足以评估文字能否“恰当”地分布在印章上，所以，我们就可以尝试用周长来进行比较。按照微积分的思想，我们可以粗略地认为，每个字符的宽度累加起来，其总和就约等于对应的这段孤线的长度。在这种情况下，我们可以考虑使用弧长公式和椭圆的周长公式。当文字宽度小于周长时，表明字体还可以放大一点；当文字宽度大于周长时，表明字体还可以缩小一点。类似地，这里给出一个基本实现：

float ScaleFontSizeByPerimeter(Graphics g, string text, Font font, float radius, float angle) {
    var fontSize = font.Size;
    
    // 圆形周长公式
    var perimeter = angle * Math.PI * radius / 180;

    // // 椭圆周长公式
    // var h = Math.Pow((a - b) / (a + b), 2);
    // var c = Math.PI * (a + b) * (1 + (3 * h / (10 + (4 - 3 * h))));
    // var perimeter = c * angle / 360;

    // 对字体缩小时需要考虑最小的字体大小
    var measuredSize = g.MeasureString(text, new Font(font.FontFamily, fontSize));
    while (measuredSize.Width > perimeter) {
        fontSize -= 0.1f;
        if (fontSize <= MIN_FONT_SIZE) break;
        measuredSize = g.MeasureString(text, new Font(font.FontFamily, fontSize));
    }

    // 对字体放大时需要考虑高度的问题
    measuredSize = g.MeasureString(text, new Font(font.FontFamily, fontSize));
    while (measuredSize.Width < perimeter) {
        fontSize += 0.1f;
        if (fontSize >= MAX_FONT_SIZE) break;
        measuredSize = g.MeasureString(text, new Font(font.FontFamily, fontSize));
    }

    return fontSize;
}

如图所示，下图展示了相同尺寸下，文字根据字数的多少按不同的字号动态进行缩放：

本文小结

写这篇博客时，其实是在一个多事之秋。如果是指新海诚的新电影《铃芽之旅》，我大概会写遗憾以及自我和解；如果是指 ChatGPT，我大概会写我对于人工智能的看法；如果是指景甜和张继科这对分手了的男女朋友，我大概会写我对于人类情感的理解；如果是指中国电科的离职事件，我大概会写我对生产力/生产关系的想法……可当很多东西纠缠在一起的时候，任何一种情绪注定都无法独自存活下去，所以，我还是决定写一点可以掌控的事物。如彼得·帕克所言，“比魔法更神奇的东西是数学”，在一个不确定性远大于确定性的时代，能够再次感受到数学世界的美好实在是一种幸运，因为一切的公式/定理都会引导你通往某个确定的地方，正如当我画完圆形印章以后，我可以快速地画出椭圆形印章，它不会增加一丝一毫的心智上的负担，而人类热衷于构建的业务流程，则永远都存在着这样那样的缺陷。也许，直到这一刻，我才能够明白科学家们渴望用一个公式描述这个世界的偏执。因为，在一个不确定的世界里寻找确定，这件事情本身就足够迷人，就像你输入到 AI 模型里的一个个提示词，它们本身或许是随机的、不确定的，可你需要的可能是一个确定的结果。毕竟，这个世界早就复杂到连选择本身都是一件困难重重的事情，对吧？